记录 CNN 学习过程中一些知识点

卷积参数与卷积结果的计算规则

# 输入数据的形状（N，Cin，Hin，Win），输出的形状（N，Cout，Hout，Wout）依次为，批次||通道||高||宽
Hin = 81
Win = 81
pad = [0,0]  # 补 0 操作，默认为 0
dilation = [1,1]  # 卷积核中每个元素的 间隔，默认为 1
kernel_size = [3, 3]  # 卷积核大小，h*w
stride = [1,1]  # 卷积核步长 默认为 1

Hout=(Hin+2*pad[0]-dilation[0]*(kernel_size[0]-1)-1)/(stride[0])+1
Wout=(Win+2*pad[1]-dilation[1]*(kernel_size[1]-1)-1)/(stride[1])+1

print(Hout,Wout)

在卷积网络中，如何设置卷积层的卷积大小是一个关键的问题，在 Inception 网络中卷积层包和多个不同大小的卷积操作，称为 Inception 模块。Inception 网络是由有多个 Inception 模块核少量的汇聚层堆叠而成。

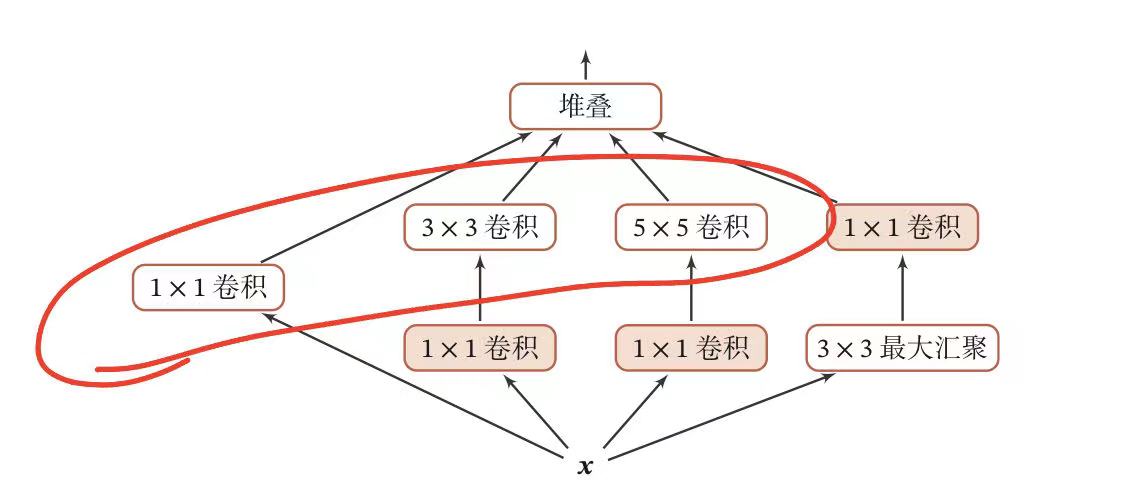
V1 版本的 Inception 模块结构，采用了 4 组平行的特征抽取方式，分别为 1x1 , 3x3 , 5x5 的卷积核 3x3 的最大汇聚。同时为了提高计算效率，减少参数数量，Inception 模块在进行 3x3，5x5 的卷积之前、3x3 的最大汇聚之后，进行一次 1x1 的卷积来减少特征的映射的深度。如果输入特征映射之间存在冗余信息，1x1 的卷积相当于先进行一次特征提取。

残差网络

残差网络 （Residual Network，ResNet）通过给非线性的卷积层增加直连边（Shortcut COnnection）的方式来提高信息的传播效率。 假设在一个深度网络中，我们期望一个非线性单元（可以为一层或多层的卷积层）$f(x;\theta)$ 去逼近一个目标函数为 h(x) ，如果将目标函数拆分成两部分： 恒等函数x 和 残差函数 h(x)-x

$$h(x)=\underset{恒等函数}{x} + \underset{残差函数}{h(x)-x}$$

用神经网络去逼近残差函数，网络更容易学习。因此，优化问题可以转换为：让非线性单元 $f(x;\theta)$ 去近似残差函数 h(x)-x ,并用 $f(x;\theta)+x$ 去逼近 x。